Contents

Vectors and Matrices

Vectors

  • A vector has magnitude (size) and direction

  • Use NumPy to create a one-dimensional array

  • Vector can be created as row or column using NumPy

vectors

See More

  • https://www.mathsisfun.com/algebra/vectors.html

  • https://en.wikipedia.org/wiki/Euclidean_vector

# Load NumPy Library 
import numpy as np 

# Create a vector as row 
vector_row = np.array([1, 2, 3])
print(vector_row)

# Create a vector as column 
vector_column = np.array([[1], [2], [3]]) 
print(vector_column)

Matrix

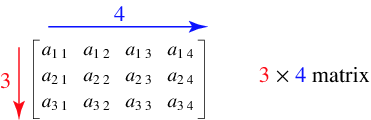
  • In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions, arranged in rows and columns

  • Rows tun horizontally and columns run vertically

  • Use NumPy to create a two-dimensional array

matrix

Matrix Order

  • You can think of an \(r x c\) matrix as a set of r row vectors, each having c elements; or you can think of it as a set of c column vectors, each having r elements.

  • The rank of a matrix is defined as (a) the maximum number of linearly independent column vectors in the matrix or (b) the maximum number of linearly independent row vectors in the matrix. Both definitions are equivalent.

  • If r is less than c, then the maximum rank of the matrix is r.

  • If r is greater than c, then the maximum rank of the matrix is c. matrix

See More

  • https://en.wikipedia.org/wiki/Matrix_(mathematics)

  • https://mathworld.wolfram.com/Matrix.html

  • https://stattrek.com/matrix-algebra/matrix-rank.aspx

Create a matrix using matrix()

  • Returns a matrix from an array type object ir string of data.

  • Syntax: np.matrix(data)

mat1 = np.matrix("1, 2, 3, 4; 4, 5, 6, 7; 7, 8, 9, 10")
print(mat1)

Create a using array()

  • Returns a matrix

  • Syntax: np.array(object)

mat2 = np.array([[1, 2], [3,4], [4, 6]])
print(mat2)

Matrix Properties

Shape

  • Returns number of rows and columns from a matrix

  • Syntax: mat.shape

    • shape[0] - returns the number of rows

    • shape[1] - returns the number of columns

mat3 = np.matrix("1, 2, 3, 4; 4, 5, 6, 7; 7, 8, 9, 10")

# shape 
mat3.shape

# rows 
mat3.shape[0]

# columns 
mat3.shape[1]

Size

  • Returns the number of elements from a matrix

  • Syntax: array.size

mat4 = np.matrix("1, 2, 3, 4; 4, 5, 6, 7; 7, 8, 9, 10")

# size 
mat4.size

Modifying matrix using insert()

  • Adds values at a given position and axis in a matrix

  • Syntax: np.insert(matrix, object, values, axis)

    • matrix - input matrix

    • object - index position

    • values - matrix of values to be inserted

mat5 = np.matrix("1, 2, 3, 4; 4, 5, 6, 7; 7, 8, 9, 10")
print(mat5)

# adding a new matrix `col_new` as a new column to mat5
col_new = np.matrix("1, 1, 1")
print(col_new)

# insert at column 
mat6 = np.insert(mat5, 0, col_new, axis=1)
print(mat6) 

# adding a new matrix `row_new` as a new row to mat5
row_new = np.matrix("0, 0, 0, 0")
print(row_new)

# insert at row 
mat7 = np.insert(mat5, 0, row_new, axis=0)
print(mat7)

Modifying matrix using index

  • Elements of matrix can be modified using index number

  • Syntax:: mat[row_index, col_index)

mat_a = np.matrix("1, 2, 3, 4, 5; 5, 6, 7, 8, 9; 9, 10, 11, 12, 13")
print(mat_a)

# change 6 with 0 
mat_a[1, 1] = 0 

# show mat_a 
print(mat_a)

# extract 2nd row 
mat_a[1, :]

# extract 3rd column
mat_a[:, 2]

# extract elements 
mat_a[1, 2]

Matrix Operations

A = np.arange(0, 20).reshape(5,4)
print(A)

B = np.arange(20, 40).reshape(5,4)
print(B)

Addition

  • np.add()- performs element-wise addition between two matrices

  • Syntax: np.add(matrix_1, matrix_2)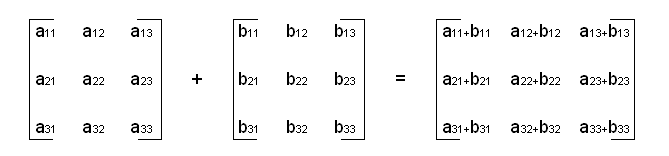 add

# addition 
np.add(A, B)

Subtraction

  • np.subtract() - performs element-wise subtraction between two matrices.

  • Syntax: np.subtract(matrix_1, matrix_2)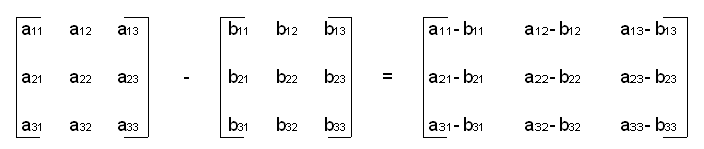 sub

Transpose

  • np.transpose() - Permute the dimensions of an array.

  • Transposing an \(M \times N\) matrix flips it around the center diagonal and results in an \(N \times M\) matrix.

  • Syntax: np.transpose(matrix)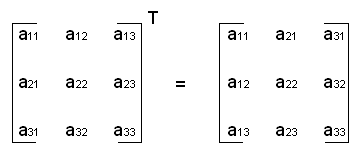 transpose

A = np.arange(0, 20).reshape(5,4)
print(A)

# transpose 
np.transpose(A)

Multiplication

  • np.dot() - performs matrix multiplication between two matrices.

  • Syntax: np.dot(matrix_1, matrix_2) mul

# multiplication
np.dot(A,B)

Note

  • For matrix multiplication the number of columns in matrix \(A\) should be equal to the number of rows in matrix \(B\)

  • Here, Order of matrix \(A\) = \(5 \times 4\) and order of matrix \(B\) = \(5 \times 4\)

  • So, \(5 \neq 4\)

  • That’s why it shows ValueError: shapes (5,4) and (5,4) not aligned: 4 (dim 1) != 5 (dim 0)

# transpose matrix B to make it 4x5 in dimension
T = np.transpose(B)
print(T)

# now we can perform multiplication
np.dot(A,T)

# using matmul 
np.matmul(A, T)

# using @ operator 
A @ T

Element-wise multiplication

  • np.multiply() - performs element-wise multiplication between two matrices.

  • Syntax: np.multiply(matrix1, matrix2)

# element-wise multiplication 
np.multiply(A, B)

Division

  • np.divide() - performs element-wise division between two matrices.

  • Syntax: np.divide(matrix_1, matrix_2)

# division
np.divide(A, B)
Universal Functions Statistics